Question:
A vessel of depth $2 \mathrm{~h}$ is half filled with a liquid of refractive index $2 \sqrt{2}$ and the upper half with another liquid of refractive index $\sqrt{2}$. The liquids are immiscible. The apparent depth of the inner surface of the bottom of vessel will be:
Correct Option: 4
Solution:
(4) Apparent depth,
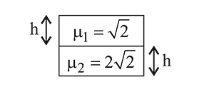
$D=\frac{t_{1}}{\mu_{1}}+\frac{t_{2}}{\mu_{2}}=\frac{h}{\sqrt{2}}+\frac{h}{2 \sqrt{2}}=\frac{3 h}{2 \sqrt{2}}=\frac{3 h \sqrt{2}}{4}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.