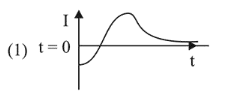
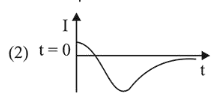
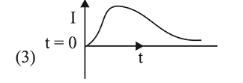
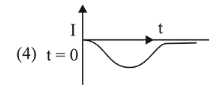
A very long solenoid of radius $R$ is carrying current $\mathrm{I}(\mathrm{t})=\mathrm{kte}^{-\alpha t}(k>0)$, as a function of time $(t \geq 0)$. Counter clockwise current is taken to be positive. A circular conducting coil of radius $2 R$ is placed in the equatorial plane of the solenoid and concentric with the solenoid. The current induced in the outer coil is correctly depicted, as a function of time, by:
Correct Option: 1
(1) $Q=B A$
$=\left(\mu_{0} n_{i}\right) A$
$=\mu_{0} n\left(k t e^{-\alpha t}\right) A$
$e=-\frac{d Q}{d t}$
$=-\mu_{0} n A k \frac{d}{d t}\left(t e^{-\alpha t}\right)$
$=-\mu_{0} n A k\left[t(-1) e^{-\alpha t}+e^{-\alpha t} \times 1\right]$
$=-\mu_{0} n A k\left[e^{-\alpha t}(1-t)\right]$
$i=\frac{e}{R}=\frac{-\mu_{0} n A k}{R}\left[e^{-\alpha t}(1-t)\right]$
At $t=0, i \Rightarrow-\mathrm{ve}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.