A vertical stick of length 7.5 m casts a shadow 5 m long on the ground and at the same time a tower casts a shadow 24 m long.

Let AB be the vertical stick and BC be its shadow.
Given:
AB = 7.5 m, BC = 5 m

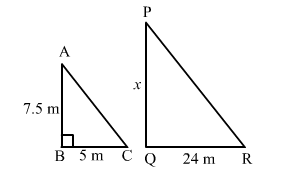
Let PQ be the tower and QR be its shadow.
Given:
QR = 24 m
Let the length of PQ be x m. 

In $\triangle A B C$ and $\triangle P Q R$ we have:

$\angle A B C=\angle P Q R=90^{\circ}$

$\angle A C B=\angle P R Q$ (Angular elevation of the Sun at the same time)

Therefore, by AA similarity theorem, we get:

$\triangle A B C \sim \triangle P Q R$

$\Rightarrow \frac{A B}{B C}=\frac{P Q}{Q R}$

$\Rightarrow \frac{7.5}{5}=\frac{x}{24}$

$\Rightarrow x=\frac{7.5}{5} \times 24=36 \mathrm{~m}$

Therefore, PQ = 36 m

Hence, the height of the tower is 36 m.