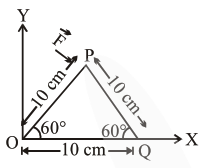
A triangular plate is shown. A force $\overrightarrow{\mathrm{F}}=4 \hat{\mathrm{i}}-3 \hat{\mathrm{j}}$ is applied at point $\mathrm{P}$. The torque at point $\mathrm{P}$ with respect to point ' $O^{\prime}$ and ' $Q$ ' are :
Correct Option: 1
$\overrightarrow{\mathrm{F}}=4 \hat{\mathrm{i}}-3 \hat{\mathrm{j}}$
$\overrightarrow{\mathrm{r}}_{1}=5 \hat{\mathrm{i}}+5 \sqrt{3} \hat{\mathrm{j}} \& \overrightarrow{\mathrm{r}}_{2}=-5 \hat{\mathrm{i}}+5 \sqrt{3} \hat{\mathrm{j}}$
Torque about 'O'
$\vec{\tau}_{\mathrm{O}}=\overrightarrow{\mathrm{r}}_{1} \times \overrightarrow{\mathrm{F}}=(-15-20 \sqrt{3}) \hat{\mathrm{k}}=(15+20 \sqrt{3})(-\hat{\mathrm{k}})$
Torque about 'Q'
$\vec{\tau}_{\mathrm{Q}}=\overrightarrow{\mathrm{r}}_{2} \times \overrightarrow{\mathrm{F}}=(-15+20 \sqrt{3}) \hat{\mathrm{k}}=(15-20 \sqrt{3})(-\hat{\mathrm{k}})$
