A triangle if its perimeter is 10.4 cm

Let ABC be a triangle. Then, given perimeter = 10.4 cm i.e., AB+ BC + CA = 10.4 cm and two angles are 45° and 120°.

say ∠B = 45° and ∠C = 120°

Now, to construct the ΔABC use the following steps.

1. Draw a line segment say $X Y$ and equal to perimeter i.e., $A B+B C+C A=10.4 \mathrm{~cm}$

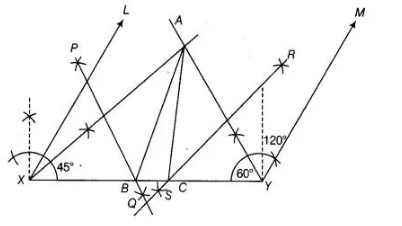
2. Make angle $\angle L X Y=\angle B=45^{\circ}$ and $\angle M Y X=\angle C=120^{\circ}$.

3. Bisect $\angle L X Y$ and $\angle M Y X$ and let these bisectors intersect at a point $A$ (say).

4. Draw perpendicular bisectors $P Q$ and $R S$ of $A X$ and $A Y$, respectively.

5. Let $P Q$ intersect $X Y$ at $B$ and $R S$ intersect $X Y$ at $C$. Join $A B$ and $A C$. Thus, $\triangle A B C$ is the required triangle.

Justification

Since, B lies on the perpendicular bisector PQ of AX.

Thus, AB+ BC + CA = XB+ BC + CY=XY

Again, ∠BAX = ∠AXB [∴ in ΔAXB, AB = XB] …(i)

Also, ∠ABC = ∠BAX + ∠AXB [ ∠ABC is an exterior angle of ΔAXB]

= ∠AXB + ∠AXB [from Eq. (i)]

= 2 ∠AXB= ∠LXY [ AX is a bisector of ∠LXB]

Also, ∠CAY = ∠AYC [∴ in A AYC, AC = CY]

∠ACB=∠CAY + ∠AYC [ ∠ACB is an exterior angle of ΔAYC]

= ∠CAY + ∠CAY

= 2 ∠CAY= ∠MYX [∴ AY is a bisector of ∠MYX]

Thus, our construction is justified.