A triangle has sides 5 cm, 12 cm and 13 cm.

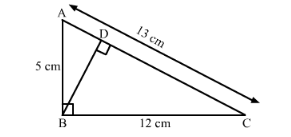
Since $B D \perp A C$ we obtained two right angled triangles, $\triangle A B D$ and $\triangle B D C$.

In $\triangle A B C$ and $\triangle A B D$

$\angle A=\angle A \quad$ (Common angle)

$\angle B=\angle D$

So, by AA-criterion $\triangle A B C \sim \triangle A D B$

$\therefore \frac{\mathrm{AB}}{\mathrm{AD}}=\frac{\mathrm{BC}}{\mathrm{BD}}=\frac{\mathrm{AC}}{\mathrm{AB}}$

$\therefore \frac{\mathrm{BC}}{\mathrm{BD}}=\frac{\mathrm{AC}}{\mathrm{AB}}$

Now we will multiply both sides of the equation by $A B \times B D$.

$B C \times A B=B D \times A C$$. .(1)$

Let us simplify the equation (1) as given below,

$B D=\frac{B C \times A B}{A C}$

Now we will substitute the values of BC, AB and AC.

$B D=\frac{12 \times 5}{13}$

$\therefore B D=\frac{60}{13}$

$\therefore B D=4.6 \mathrm{~cm}$

Therefore, the length of the altitude is $4.6 \mathrm{~cm}$