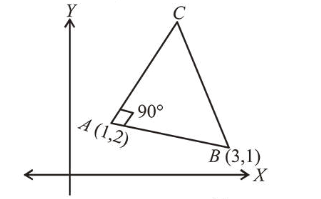
A triangle $A B C$ lying in the first quadrant has two vertices as $A(1,2)$ and $B(3,1)$. If $\angle B A C=90^{\circ}$, and ar $(\triangle A B C)=5 \sqrt{5}$ sq. units, then the abscissa of the vertex $C$ is:
Correct Option: , 2
Let $\triangle A B C$ be in the first quadrant
Slope of line $A B=-\frac{1}{2}$
Slope of line $A C=2$
Length of $A B=\sqrt{5}$
It is given that $\operatorname{ar}(\triangle A B C)=5 \sqrt{5}$
$\therefore \frac{1}{2} A B \cdot A C=5 \sqrt{5} \Rightarrow A C=10$
$\therefore$ Coordinate of vertex $C=(1+10 \cos \theta, 2+10 \sin \theta)$
$\because \tan \theta=2 \Rightarrow \cos \theta=\frac{1}{\sqrt{5}}, \sin \theta=\frac{2}{\sqrt{5}}$
$\therefore$ Coordinate of $\mathrm{C}=(1+2 \sqrt{5}, 2+4 \sqrt{5})$
$\therefore$ Abscissa of vertex $C$ is $1+2 \sqrt{5}$
Comments
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.