A tree breaks due to storm and the broken part bends so that the top of the tree touches

Let AB be the tree of height h. And the top of tree makes an angle 30° with ground. The distance between foot of tree to the point where the top touches is 8m. Let. And.

Here we have to find height of tree.

So we trigonometric ratios

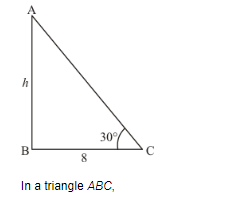
$\Rightarrow \quad \tan C=\frac{A B}{B C}$

$\Rightarrow \quad \tan 30^{\circ}=\frac{A B}{B C}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{h}{8}$

$\Rightarrow \quad h=\frac{8}{\sqrt{3}}$

Now in triangle ABC

$\sin 30^{\circ}=\frac{A B}{A C}$

$\Rightarrow \quad \frac{1}{2}=\frac{h}{A C}$

$\Rightarrow \quad \frac{1}{2}=\frac{\frac{8}{\sqrt{3}}}{A C}$

$\Rightarrow \quad A C=\frac{16}{\sqrt{3}}$

So the height of the tree is 

$h+A C=\frac{8}{\sqrt{3}}+\frac{16}{\sqrt{3}}$

$=8 \sqrt{3}$

Hence the height of tree is $\mathrm{m}$.