A transversal intersects two parallel lines.

Given Two lines AB and CD are parallel and intersected by transversal t at P and 0, respectively. Also, EP and FQ are the bisectors of angles ∠APG and  ∠CQP, respectively.

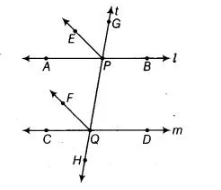
To prove $E P \| F Q$

Proof Given, $A B \| C D$

$\Rightarrow \quad \angle A P G=\angle C Q P$ [corresponding angles]

$\Rightarrow$ $\frac{1}{2} \angle A P G=\frac{1}{2} \angle C Q P$ [dividing both sides by 2]

 $\Rightarrow$ $\angle E P G=\angle F Q P$

$[\because E P$ and $F Q$ are the bisectors of $\angle A P G$ and $\angle C Q P$, respectively]

As these, are the corresponding angles on the transversal line $t$.

$\therefore \quad E P \| F Q$ 

Hence proved.