A toy is in the shape of a cone mounted on a hemisphere of same base radius

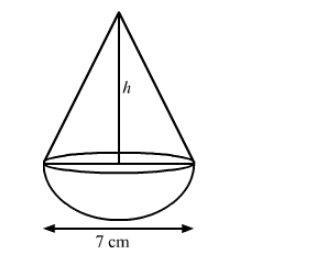
We have,

Base radius of cone $=$ Base radius of hemisphere $=r=\frac{7}{2}=3.5 \mathrm{~cm}$,

As, the volume of the toy $=231 \mathrm{~cm}^{3}$

$\Rightarrow$ Volume of cone $+$ Volume of hemisphere $=231$

$\Rightarrow \frac{1}{3} \pi r^{2} h+\frac{2}{3} \pi r^{3}=231$

$\Rightarrow \frac{1}{3} \pi r^{2}(h+2 r)=231$

$\Rightarrow \frac{1}{3} \times \frac{22}{7} \times 3.5 \times 3.5 \times(h+2 \times 3.5)=231$

$\Rightarrow \frac{38.5}{3} \times(h+7)=231$

$\Rightarrow h+7=\frac{231 \times 3}{38.5}$

$\Rightarrow h+7=18$

$\Rightarrow h=18-7$

$\Rightarrow h=11 \mathrm{~cm}$

So, the height of the toy $=h+r=11+3.5=14.5 \mathrm{~cm}$