A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius.

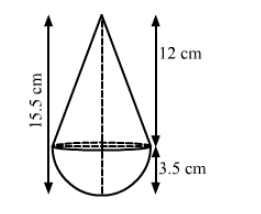
We have,

Radius of the hemisphere $=$ Radius of the cone $=r=3.5 \mathrm{~cm}$ and

Height of the cone $=15.5-3.5=12 \mathrm{~cm}$

Also,

The slant height of the cone, $l=\sqrt{h^{2}+r^{2}}$

$=\sqrt{12^{2}+3.5^{2}}$

$=\sqrt{144+12.25}$

$=\sqrt{156.25}$

$=12.5 \mathrm{~cm}$

Now,

Total surface area of the toy $=$ CSA of cone $+$ CSA of hemisphere

$=\pi r l+2 \pi r^{2}$

$=\pi r(l+2 r)$

$=\frac{22}{7} \times 3.5 \times(12.5+2 \times 3.5)$

$=11 \times(12.5+7)$

$=11 \times 19.5$

$=214.5 \mathrm{~cm}^{2}$

So, the total surface area of the toy is 214.5 cm2.

Disclaimer: The answer given in the textbook is incorrect. The same has been corrected above.