A tower subtends an angle of 30° at a point on the same level as its foot.

Let AB be the tower and C is a point on the same level as its foot such that ∠ACB = 30°

The given situation can be represented as,

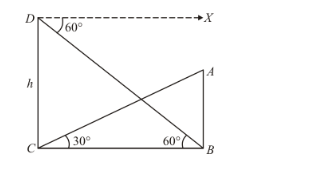
Here D is a point h m above the point C.

In ΔBCD,

$\Rightarrow \tan B=\frac{C D}{C B}$

$\Rightarrow \tan 60^{\circ}=\frac{h}{C B}$

$\Rightarrow \sqrt{3}=\frac{h}{C B}$

$\Rightarrow C B=\frac{h}{\sqrt{3}}$

Again in triangle ABC,

$\tan C=\frac{A B}{C B}$

$\Rightarrow \tan 30^{\circ}=\frac{A B}{\left(\frac{h}{\sqrt{3}}\right)} \quad[$ Using (1) $]$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{A B}{\left(\frac{h}{\sqrt{3}}\right)}$

$\Rightarrow A B=\frac{h}{3}$

Hence the correct option is $c$.