A tower stands vertically on the ground. From a point on the ground which is 20 m

Let AB">AB be the tower standing vertically on the ground and O be the position of the observer.
We now have:

$O A=20 m, \angle O A B=90^{\circ}$ and $\angle A O B=60^{\circ}$

Let:

$A B=h \mathrm{~m}$

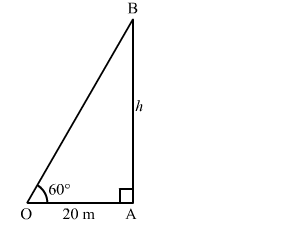
Now, in the right $\Delta O A B$, we have:

$\frac{A B}{O A}=\tan 60^{\circ}=\sqrt{3}$

$\Rightarrow \frac{h}{20}=\sqrt{3}$

$\Rightarrow h=20 \sqrt{3}=(20 \times 1.732)=34.64$

Hence, the height of the pole is 34.64 m.