Question:
A tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower.
Solution:
Given a tower at the ground such that at a distance of 20 m away from foot of tower,
the top of tower makes an angle of 
with the ground.
We have to find the height of the tower.
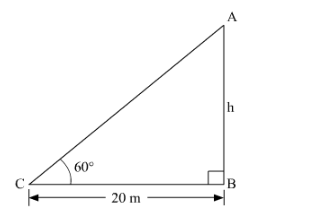
Let the tower be AB
Height of the tower = h
Distance of the tower from point C where top of the tower makes an angle of = 20 m
Since B is the foot of the tower, CB = 20 m
$\angle A C B=60^{\circ}$
In $\triangle A B C$
$\frac{A B}{B C}=\tan 60^{\circ}$
$\frac{h}{20}=\sqrt{3}$
$h=20 \sqrt{3}$
Height of the tower $=20 \sqrt{3}$