A tent is of the shape of a right circular cylinder

Solution:

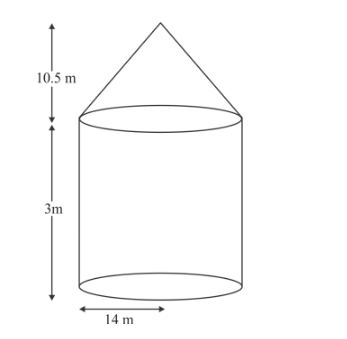
Let r m be the radius of cylindrical base of cylinder of height by m

r = 14 m and h1 = 3m

Curved surface area of cylinder

$=2 \pi r h_{1} m^{2}$

$=25 \frac{22}{7} \times 14 \times 3 \mathrm{~m}^{2}$

$=264 \mathrm{~m}^{2}$

The radius of cylindrical box of cylinder is also equal to the radius of right circular cons.

Let h2 be the height of cone and l be the slant height of cone

$r=14 m$ and $h_{2}=(13.5-3)$

$=10.5 \mathrm{~m}$

$l^{2}=r^{2}+h_{2}^{2}$

$l^{2}=(14)^{2}+(10.5)^{2}$

 

$l^{2}=(14)^{2}+(10.5)^{2}$

$I=\sqrt{196+110.25}$

$\sqrt{306.25}=17.5 \mathrm{~m}$

Curved surface area of the cone

$=\pi r l$

$=\frac{22}{7} \times 14 \times 17.5$

$=770 \mathrm{~m}^{2}$

Therefore,

Total area of tent which is to be painted

= curved surface area of cylinder + curved surface area of cone

$=(264+770) \mathrm{m}^{2}$

$=1034 \mathrm{~m}^{2}$

Now cost of painting 1 m2 of inner side of tent = Rs. 2

Cost of painting 1034 m2 inner side of tent

$=2 \times 1034$

$=$ Rs. 2068