A student records the initial length l, change in temperature ∆T and change in length ∆l of a rod as follows:
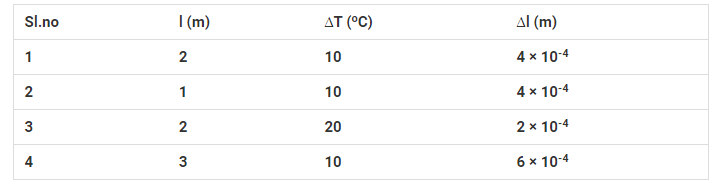
If the first observation is correct, what can you say about observations 2, 3, and 4.
It is given that the first observation is correct which means that the coefficient of linear expansion is
$\alpha=\frac{\Delta l}{l \times \Delta T}=\frac{4 \times 10^{-4}}{2 \times 10}=2 \times 10^{-50} \mathrm{C}^{-1}$
For second observation,
$\Delta l=\alpha l \Delta T=2 \times 10^{-4} m \neq 4 \times 10^{-4} m$
Which is incorrect
For third observation,
$\Delta l=\alpha l \Delta T=8 \times 10^{-4} \mathrm{~m} \neq 2 \times 10^{-4} \mathrm{~m}$
Which is incorrect
For fourth observation,
$\Delta l=\alpha l \Delta T=6 \times 10^{-4} \mathrm{~m}=6 \times 10^{-4} \mathrm{~m}$
Which is correct
