A straight highway leads to the foot of a tower.

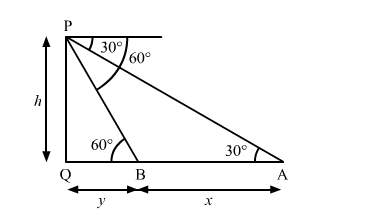
Let PQ be the tower.

We have,

$\angle \mathrm{PBQ}=60^{\circ}$ and $\angle \mathrm{PAQ}=30^{\circ}$

Let $\mathrm{PQ}=h, \mathrm{AB}=x$ and $\mathrm{BQ}=y$

In $\triangle \mathrm{APQ}$,

$\tan 30^{\circ}=\frac{\mathrm{PQ}}{\mathrm{AQ}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{x+y}$

$\Rightarrow x+y=h \sqrt{3} \quad \ldots$ (i)

Also, in $\triangle \mathrm{BPQ}$,

$\tan 60^{\circ}=\frac{\mathrm{PQ}}{\mathrm{BQ}}$

$\Rightarrow \sqrt{3}=\frac{h}{y}$

$\Rightarrow h=y \sqrt{3} \quad \ldots$ (ii)

Substituting $h=y \sqrt{3}$ in (i), we get

$x+y=\sqrt{3}(y \sqrt{3})$

$\Rightarrow x+y=3 y$

$\Rightarrow 3 y-y=x$

$\Rightarrow 2 y=x$

$\Rightarrow y=\frac{x}{2}$

As, speed of the car from A to B $=\frac{\mathrm{AB}}{6}=\frac{x}{6}$ units / sec

So, the time taken to reach the foot of the tower i.e. $\mathrm{Q}$ from $\mathrm{B}=\frac{\mathrm{BQ}}{\text { speed }}$

$=\frac{y}{\left(\frac{x}{6}\right)}$

$=\frac{\left(\frac{x}{2}\right)}{\left(\frac{x}{6}\right)}$

$=\frac{6}{2}$

$=3 \mathrm{sec}$

So, the time taken to reach the foot of the tower from the given point is 3 seconds.