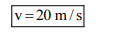Question:
A stone of mass $20 \mathrm{~g}$ is projected from a rubber catapult of length $0.1 \mathrm{~m}$ and area of cross section $10^{-6} \mathrm{~m}^{2}$ stretched by an amount $0.04 \mathrm{~m}$. The velocity of the projected stone is $\mathrm{m} / \mathrm{s}$.
(Young's modulus of rubber $=0.5 \times 10^{9} \mathrm{~N} / \mathrm{m}^{2}$ )
Solution:
By energy conservation
$\frac{1}{2} \cdot \frac{\mathrm{YA}}{\mathrm{L}} \cdot \mathrm{x}^{2}=\frac{1}{2} \mathrm{mv}^{2}$
$\frac{0.5 \times 10^{9} \times 10^{-6} \times(0.04)^{2}}{0.1}=\frac{20}{1000} \mathrm{v}^{2}$
$\therefore v^{2}=400$