A square is inscribed in an isosceles right triangle so that the square and the triangle have one angle common.

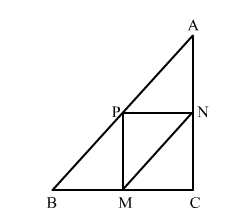
Given: In an isosceles right ∆ABC, CMPN is a square.
 
To prove: P bisects the hypotenuse AB i.e., AP = PB.
 
Proof:

In square CMPN,
 
∴ CM = MP = PN = CN            (All sides are equal.)
 
Also, ∆ABC is an isosceles with AC = BC.

⇒ AN + NC = CM + MB

⇒ AN = MB          (∵ CN = CM)       ...(i)

Now,

In ∆ANP and ∆PMB,

AN = MB                [From (i)]

∠ANP = ∠PMB = 90°

PN = PM             (Sides of square CMPN)

∴ By SAS congruence criteria,

∆ANP ≅ ∆BMP

Hence, AP = PB         (By CPCT)