Question:
A square is inscribed in an isosceles right triangle, so that the square and the triangle have one angle common. Show that the vertex of the square
opposite the vertex of the common angle bisects the hypotenuse.
Solution:
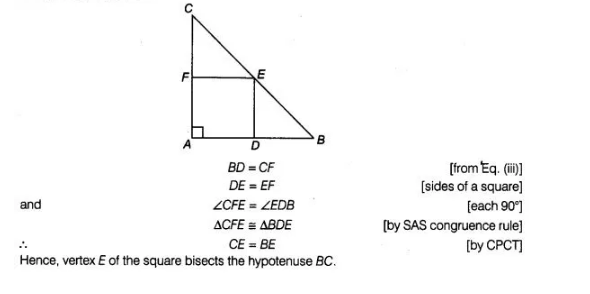
Given In isosceles triangle ABC, a square ΔDEF is inscribed.
To prove CE = BE
Proof In an isosceles ΔABC, ∠A = 90°
and AB=AC …(i)
Since, ΔDEF is a square.
AD = AF [all sides of square are equal] … (ii)
On subtracting Eq. (ii) from Eq. (i), we get
AB – AD = AC- AF
BD = CF ….(iii)
Now, in $\triangle C F E$ and $\triangle B D E$,