Question:
A source and a detector move away from each other in absence of wind with a speed of $20 \mathrm{~m} / \mathrm{s}$ with respect to the ground. If the detector detects a frequency of $1800 \mathrm{~Hz}$ of the sound coming from the source, then the original frequency of source considering speed of sound in air $340 \mathrm{~m} / \mathrm{s}$ will be $\mathrm{Hz}$
Solution:
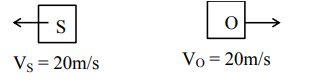
$f^{\prime}=f\left(\frac{C-V_{0}}{C+V_{s}}\right)$
$1800=f\left(\frac{340-20}{340+20}\right)$
$f=2025 \mathrm{~Hz}$
Ans. 2025
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.