A solid metallic right circular cone 20 cm high and whose vertical angle is 60°,

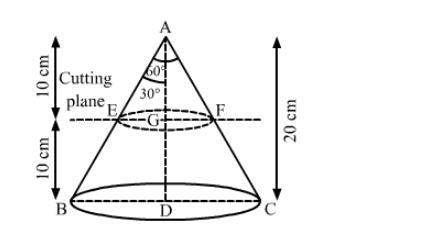
We have,

Height of the solid metallic cone, $H=20 \mathrm{~cm}$,

Height of the frustum, $h=\frac{20}{2}=10 \mathrm{~cm}$ and

Radius of the wire $=\frac{1}{24} \mathrm{~cm}$

Let the length of the wire be $l, \mathrm{EG}=r$ and $\mathrm{BD}=R$.

In $\triangle \mathrm{AEG}$,

$\tan 30^{\circ}=\frac{\mathrm{EG}}{\mathrm{AG}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{r}{H-h}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{r}{20-10}$

$\Rightarrow r=\frac{10}{\sqrt{3}} \mathrm{~cm}$

Also, in $\triangle \mathrm{ABD}$,

$\tan 30^{\circ}=\frac{\mathrm{BD}}{\mathrm{AD}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{R}{H}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{R}{20}$

$\Rightarrow R=\frac{20}{\sqrt{3}} \mathrm{~cm}$

Now,

Volume of the wire = Volume of the frustum

$\Rightarrow \pi\left(\frac{1}{24}\right)^{2} l=\frac{1}{3} \pi h\left(R^{2}+r^{2}+R r\right)$

$\Rightarrow \frac{l}{576}=\frac{1}{3} \times 10 \times\left[\left(\frac{20}{\sqrt{3}}\right)^{2}+\left(\frac{10}{\sqrt{3}}\right)^{2}+\left(\frac{20}{\sqrt{3}}\right)\left(\frac{10}{\sqrt{3}}\right)\right]$

$\Rightarrow l=\frac{576}{3} \times 10 \times\left[\frac{400}{3}+\frac{100}{3}+\frac{200}{3}\right]$

$\Rightarrow l=\frac{576}{3} \times 10 \times \frac{700}{3}$

$\Rightarrow l=448000 \mathrm{~cm}$

$\therefore l=4480 \mathrm{~m}$

So, the length of the wire is 4480 m.