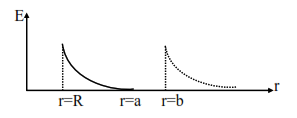
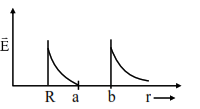
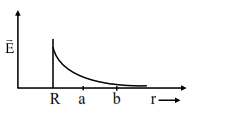
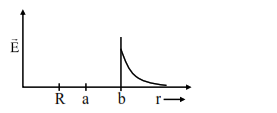
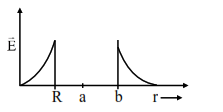
A solid metal sphere of radius $R$ having charge $q$ is enclosed inside the concentric spherical shell of inner radius $a$ and outer radius $b$ as shown in figure. The approximate variation electric field $\overrightarrow{\mathrm{E}}$ as a function of distance $r$ from centre $O$ is given by
Correct Option: 1
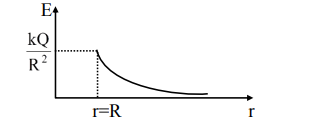
Considering outer spherical shell is nonconducting
Electric field inside a metal sphere is zero.
$\mathrm{r}<\mathrm{R} \Rightarrow \mathrm{E}=0$
$r>R \Rightarrow E=\frac{k Q}{r^{2}}$
Option (2)
Considering outer spherical shell is conducting
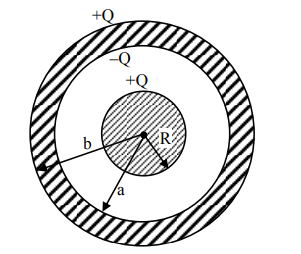
$\mathrm{r}<\mathrm{R}, \mathrm{E}=0$
$\mathrm{R} \leq \mathrm{r}<\mathrm{a}$
$\mathrm{E}=\frac{\mathrm{kQ}}{\mathrm{r}^{2}}$
$a \leq r $\mathrm{E}=0$ $r \geq b$ $\mathrm{E}=\frac{\mathrm{kQ}}{\mathrm{r}^{2}}$ Option (1)