A solid is in the form of a cylinder with hemispherical ends.

Solution:

Volume of cylinder $=\pi r^{2} h$

$=\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 12$

$=462 \mathrm{~cm}^{3}$

Volume of 2 hemisphere $=4 \pi r^{3}$

$=\frac{4}{3} \times \frac{22}{2} \times \frac{7}{2} \times \frac{7}{2} \times \frac{7}{2}$

$=179.6 \mathrm{~cm}^{3}$

Therefore,

Volume of solid $=462+179.6$

$=641.6 \mathrm{~cm}^{3}$

Total surface area of the solid

$=2 \pi r h+4 \pi r^{2}$

 

$=2 \pi r(h+2 r)$

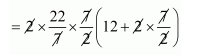
$=418 \mathrm{~cm}^{2}$