Question:
A solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is
(a) $1: 3$
(b) $1: \sqrt{3}$
(c) $1: 1$
(d) $\sqrt{3}: 1$
Solution:
Let r be the radius of the base and h be the height of conical part.
Since,
Surface area of both part of solid is equal.
i.e.,
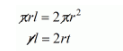
$l=2 r$ ..............$(i)$
But,
$I=\sqrt{h^{2}+r^{2}}$
Squaring on both side,
Then we get,
$l^{2}=h^{2}+r^{2}$
From equation (i) putting the value of l in above equation
$4 r^{2}=h^{2}+r^{2}$
$3 r^{2}=h^{2}$
$\frac{r}{h}=\frac{1}{\sqrt{3}}$
$r: h=1: \sqrt{3}$
Hence, the correct answer is choice (b).
