A solid cylinder of mass $m$ is wrapped with an inextensible light string and, is placed on a rough inclined plane as shown in the figure. The frictional force acting between the cylinder and the inclined plane is :
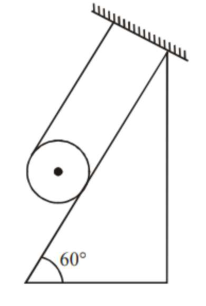
[The coefficient of static friction, $\mu_{\mathrm{s}}$, is $\left.0.4\right]$
Correct Option: , 3
(3)
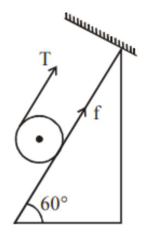
Let's take solid cylinder is in equilibrium
$\mathrm{T}+\mathrm{f}=\mathrm{mg} \sin 60 \ldots$ (i)
$\mathrm{TR}-\mathrm{fR}=0 \ldots$ (ii)
Solving we get
$\mathrm{T}=\mathrm{f}_{\mathrm{req}}=\frac{\mathrm{mg} \sin \theta}{2}$
But limiting friction $<$ required friction
$\mu \mathrm{mg} \cos 60^{\circ}<\frac{\mathrm{mg} \sin 60^{\circ}}{2}$
$\therefore$ Hence cylinder will not remain in equilibrium Hence $f=$ kinetic
$=\mu_{\mathrm{k}} \mathrm{N}$
$=\mu_{\mathrm{k}} \mathrm{mg} \cos 60^{\circ}$
$=\frac{\mathrm{mg}}{5}$
