A solid cylinder of diameter 12 cm and height 15 cm is melted and recast into toys with the shape of a right circular cone mounted on a hemisphere of radius 3 cm.If the height of the toy is 12 cm, find the number of toys so formed.
Diameter of cylinder = 12 cm
Therefore
r = 6 cm
Height = 15 cm
Therefore,
Volume of cylinder
$=\pi r^{2} h$
$=36 \times 15 \times \pi \mathrm{cm}^{3}$
Therefore,
Volume of toy = volume of cone + volume of hemisphere
$=\frac{1}{3} \pi r^{2} h+\frac{2}{3} \pi r^{3}$
$=\frac{1}{3} \pi r^{2}(h+2 r)$
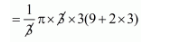
$=45 \pi \mathrm{cm}^{3}$
Therefore,
No. of toys
$=\frac{\text { volume of cylinder }}{\text { volume of toy }}$
$=\frac{36 \times 15 \times \pi}{45 \times \pi}$
$=12$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.