A solid consists of a circular cylinder with an exact fitting right circular cone placed at the top.
Question:
A solid consists of a circular cylinder with an exact fitting right circular cone placed at the top. The height of the cone is h. If the total volume of the solid is 3 times the volume of the cone, then the height of the circular is
(a) $2 h$
(b) $\frac{2 h}{3}$
(c) $\frac{3 h}{2}$
(d) $4 h$
Solution:
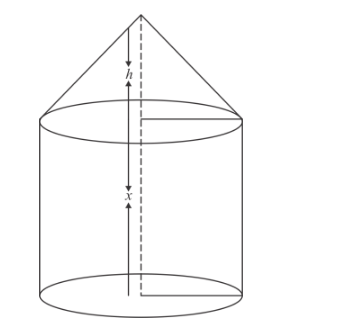
Let r be the radius of the base of solid.
Clearly,
The volume of solid = 3 × volume of cone
Vol. of cone + Vol. of cylinder = 3 Volume of cone
Vol. of cylinder = 2 Vol. of cone
$x=\frac{2}{3} h$
Thus,
The height of cylinder $=\frac{2 h}{3}$
Hence, the correct answer is choice (b).
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.