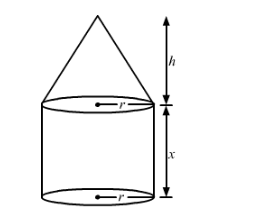
A solid consists of a circular cylinder surmounted by a right circular cone.

Disclaimer: In the the question, the statement given is incorrect. Instead of total height of solid being equal to 3 times the volume 
of cone, the volume of the total solid should be equal to 3 times the volume of the cone.

Let x be the height of cylinder.

Since, volume of the total solid should be equal to 3 times the volume of the cone, 
So,

$\frac{1}{3} \pi r^{2} h+\pi r^{2} x=3\left(\frac{1}{3} \pi r^{2} h\right)$

$\Rightarrow \frac{1}{3} \pi \mathrm{r}^{2} \mathrm{~h}-\pi \mathrm{r}^{2} \mathrm{~h}+\pi \mathrm{r}^{2} \mathrm{x}=0$

$\Rightarrow \pi r^{2} x=\frac{2}{3} \pi r^{2} h$

$\Rightarrow \mathrm{x}=\frac{2}{3} \mathrm{~h}$

Hence, the height of cylindrical part $=\frac{2 h}{3}$

Hence, the correct answer is choice (d).