A small bob tied at one end of a thin string of length $1 \mathrm{~m}$ is describing a vertical circle so that the maximum and minimum tension in the string are in the ratio $5: 1$. The velocity of the bob at the height position is_________ $\mathrm{m} / \mathrm{s}$.
(Take $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}$ )
Let the speed of bob at lowest position be $\mathrm{v}_{1}$ and at the highest position be $v_{2}$.
Maximum tension is at lowest position and minimum tension is at the highest position.
Now, using, conservation of mechanical energy,
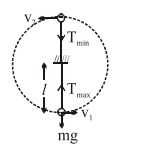
$\frac{1}{2} \mathrm{mv}_{1}^{2}=\frac{1}{2} \mathrm{mv}_{2}^{2}+\mathrm{mg} 2 l$
$\Rightarrow \mathrm{v}_{1}^{2}=\mathrm{v}_{2}{ }^{2}+4 \mathrm{gl}$......(1)
Now $\mathrm{T}_{\max }-\mathrm{mg}=\frac{\mathrm{mv}_{\perp}^{2}}{l}$
$\Rightarrow \mathrm{T}_{\max }=\mathrm{mg}+\frac{\mathrm{mv}_{1}^{2}}{l}$
$\& \mathrm{~T}_{\min }+\mathrm{mg}=\frac{\mathrm{mv}_{2}^{2}}{l}$
$\Rightarrow \mathrm{T}_{\min }=\frac{\mathrm{mv}_{2}^{2}}{l}-\mathrm{mg}$
$\frac{\mathrm{T}_{\max }}{\mathrm{T}_{\min }}=\frac{5}{1}$
$\Rightarrow \frac{\mathrm{mg}+\frac{\mathrm{mv}_{1}^{2}}{l}}{\frac{\mathrm{mv}_{2}^{2}}{l}-\mathrm{mg}}=\frac{5}{1}$
$\Rightarrow \mathrm{mg}+\frac{\mathrm{mv}_{1}^{2}}{l}=\left[\frac{\mathrm{mv}_{2}^{2}}{l}-\mathrm{mg}\right] 5$
$\Rightarrow \mathrm{mg}+\frac{\mathrm{m}}{l}\left[\mathrm{v}_{2}^{2}+4 \mathrm{~g} l\right]=\frac{5 \mathrm{mv}_{2}^{2}}{l}-5 \mathrm{mg}$
$\Rightarrow \mathrm{mg}+\frac{\mathrm{mv}_{2}^{2}}{l}+4 \mathrm{mg}=\frac{5 \mathrm{mv}_{2}^{2}}{l}-5 \mathrm{mg}$
$\Rightarrow 10 \mathrm{mg}=\frac{4 \mathrm{mv}_{2}^{2}}{l}$
$\mathrm{v}_{2}^{2}=\frac{10 \times 10 \times 1}{4}$
$\Rightarrow \mathrm{v}_{2}^{2}=25 \Rightarrow \mathrm{v}_{2}=5 \mathrm{~m} / \mathrm{s}$
Thus, velocity of bob at highest position is $5 \mathrm{~m} / \mathrm{s}$
