Question:
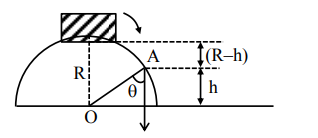
A small block slides down from the top of hemisphere of radius R = 3 m as shown in the figure. The height 'h' at which the block will lose contact with the surface of the sphere is ____m.
(Assume there is no friction between the block and the hemisphere)
Solution:
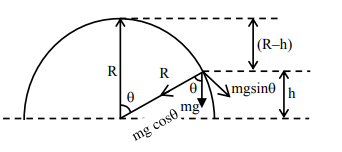
$m g \cos \theta=\frac{m v^{2}}{R}$ ......(1)
$\cos \theta=\frac{h}{R}$
Energy conservation
$m g\{R-h\}=\frac{1}{2} m v^{2}$ .....(2)
from (1) \& (2) $\Rightarrow \operatorname{mg}\left\{\frac{\mathrm{h}}{\mathrm{R}}\right\}=\frac{2 \mathrm{mg}\{\mathrm{R}-\mathrm{h}\}}{\mathrm{R}}$
$h=\frac{2 R}{3}=2 m$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.