A satellite is moving in a low nearly circular orbit around the earth. Its radius is roughly equal to that of the earth's radius $R_{e}$. By firing rockets attached to it, its speed is instantaneously increased in the direction of its motion so
that it become $\sqrt{\frac{3}{2}}$ times larger. Due to this the farthest
distance from the centre of the earth that the satellite reaches is $R$. Value of $R$ is :
Correct Option: , 2
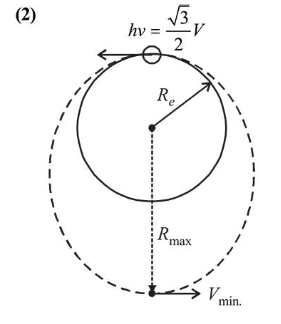
Orbital velocity, $V_{0}=\sqrt{\frac{G M}{R_{e}}}$
From energy conversation,
$-\frac{G M m}{R_{e}}+\frac{1}{2} m\left(\sqrt{\frac{3}{2}} V\right)^{2}=\frac{G M m}{R_{\max }}+\frac{1}{2} m V_{\min }^{2}$ ....(1)
From angular momentum conversation
$\sqrt{\frac{3}{2}} V R_{e}=V_{\min } R_{\max }$
Solving equation (1) and (2) we get,
$R_{\max }=3 R_{e}$
Comments
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.