A salesman has the following record of sales during three months for three items A, B and C which have different rates of commission
A salesman has the following record of sales during three months for three items A, B and C which have different rates of commission
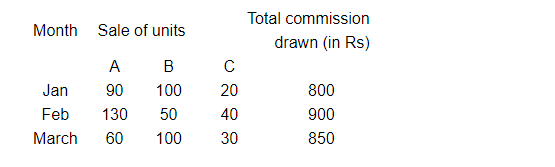
Find out the rates of commission on items A, B and C by using determinant method.
Let x, y and z be the rates of commission on items A, B and C respectively. Based on the given data, we get
$90 x+100 y+20 z=800$
$130 x+50 y+40 z=900$
$60 x+100 y+30 z=850$
$D=\left|\begin{array}{ccc}9 & 10 & 2 \\ 13 & 5 & 4 \\ 6 & 10 & 3\end{array}\right|$ [Expressing the equation as a determinant]
$=9(15-40)-10(39-24)+2(130-30)$
$=9(-25)-10(15)+2(100)$
$=-175$
$D_{1}=\left|\begin{array}{ccc}80 & 10 & 2 \\ 90 & 5 & 4 \\ 85 & 10 & 3\end{array}\right|$
$=80(15-40)-10(270-340)+2(900-425)$
$=80(-25)-10(-70)+2(475)$
$=-350$
$D_{2}=\left|\begin{array}{ccc}9 & 80 & 2 \\ 13 & 90 & 4 \\ 6 & 85 & 3\end{array}\right|$
$=9(270-340)-80(39-24)+2(1105-540)$
$=9(-70)-80(15)+2(565)$
$=-700$
$D_{3}=\left|\begin{array}{ccc}9 & 10 & 80 \\ 13 & 5 & 90 \\ 6 & 10 & 85\end{array}\right|$
$=9(425-900)-10(1105-540)+80(130-30)$
$=9(-475)-10(565)+80(100)$
$=-1925$
Thus,
$x=\frac{D_{1}}{D}=\frac{-350}{-175}=2$
$y=\frac{D_{2}}{D}=\frac{-700}{-175}=4$
$z=\frac{D_{3}}{D}=\frac{-1925}{-175}=11$
Therefore, the rates of commission on items A, B and C are 2, 4 and 11, respectively.
