Question:
A round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm, then find the total area of the design.
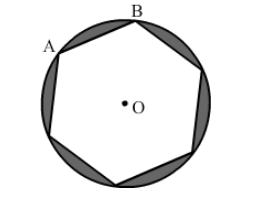
Solution:
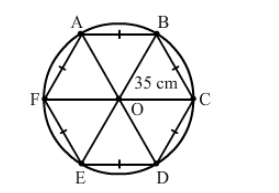
Join each vertex of the hexagon to the centre of the circle.
The hexagon is made up of six triangles.
Total area of the design = Area of the circle $-$ Area of six triangles
$=\left[\frac{22}{7} \times 35 \times 35\right]-\left[6 \times\left(\frac{\sqrt{3}}{4} \times 35 \times 35\right)\right]$
$=(35 \times 35)\left[\frac{22}{7}-\left(\frac{6 \times 1.732}{4}\right)\right]$
$=1225\left(\frac{22}{7}-2.598\right)$
$=1225 \times 0.542$
$=663.95 \mathrm{~cm}^{2}$
