A rocket is in the form of a circular cylinder closed at the lower end and a cone of the same radius is attached to the top.

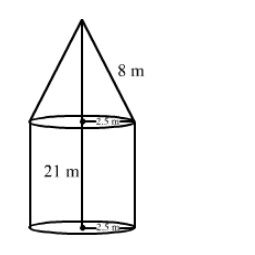
Radius of the cylinder = 2.5 m
Height of the cylinder = 21 m

Curved surface area of the cylinder $=2 \pi \mathrm{rh}=2 \times \frac{22}{7} \times 2.5 \times 21=330 \mathrm{~m}^{2}$

Radius of the cone = 2.5 m
Slant height of the cone = 8 m

Curved surface area of the cone $=\pi \mathrm{rl}=\frac{22}{7} \times 2.5 \times 8=62.86 \mathrm{~m}^{2}$

Area of circular base $=\pi \mathrm{r}^{2}=\frac{22}{7} \times 2.5 \times 2.5=19.643 \mathrm{~m}^{2}$

$\therefore$ Total surface area of rocket $=330+62.86+19.643=412.503 \mathrm{~m}^{2}$