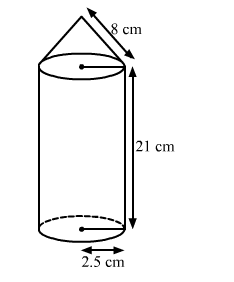
A rocket is in the form of a circular cylinder closed

Given:

Radius of the cylinder $r=2.5 \mathrm{~m}$, height of the cylinder, $h=21 \mathrm{~m}$, slant height of the cone $l=8 \mathrm{~m}$. We have to find total surface area and volume of the rocket Let us assume that the area of the cone is $S_{1}$.

$S_{1}=\pi r l$

$=3.14 \times 2.5 \times 8$

$=62.8 \mathrm{~m}^{2}$

The area of the cylinder $S_{2}$ is given by

$S_{2}=2 \pi r h+\pi r^{2}$

$=3.14 \times 2.5(2 \times 21+2.5)$

$=349.33 \mathrm{~m}^{2}$

Total areais

$S=S_{1}+S_{2}$

$=62.8+349.33$

$=412.13 \mathrm{~m}^{2}$

Now, we are going to find the volume of the rocket V.

Volume of the cone is given by

$V_{1}=\frac{1}{3} \pi r^{2} h$

$=\frac{1}{3} \times 3.14 \times 2.5^{2} \sqrt{8^{2}-2.5^{2}}$

$=49.71 \mathrm{~m}^{3}$

Volume of the cylinder is

$V_{2}=\pi r^{2} h$

$=3.14 \times 2.5^{2} \times 21$

$=412.13 \mathrm{~m}^{3}$

Total volume of the cone is given by

$V=V_{1}+V_{2}$

$=49.71+412.13$

$=461.84 \mathrm{~m}^{3}$

Hence, the area and the volume of the rocket is $S=412.13 \mathrm{~m}^{2}, \mathrm{~V}=461.84 \mathrm{~m}^{3}$