A right triangle whose sides are 15 cm and 20 cm (other than hypotenuse), is made to revolve about its hypotenuse.

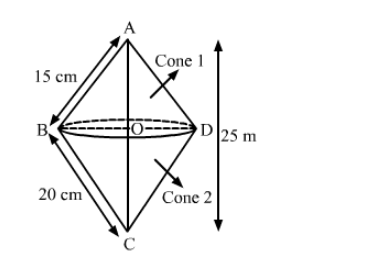
We have,

In $\Delta \mathrm{ABC}, \angle \mathrm{B}=90^{\circ}, \mathrm{AB}=l_{1}=15 \mathrm{~cm}$ and $\mathrm{BC}=l_{2}=20 \mathrm{~cm}$

Let $\mathrm{OD}=\mathrm{OB}=r, \mathrm{AO}=h_{1}$ and $\mathrm{CO}=h_{2}$

Using Pythagoras theorem,

$\mathrm{AC}=\sqrt{\mathrm{AB}^{2}+\mathrm{BC}^{2}}$

$=\sqrt{15^{2}+20^{2}}$

$=\sqrt{225+400}$

$=\sqrt{625}$

$\Rightarrow h=25 \mathrm{~cm}$

As, ar $(\Delta \mathrm{ABC})=\frac{1}{2} \times \mathrm{AC} \times \mathrm{BO}=\frac{1}{2} \times \mathrm{AB} \times \mathrm{BC}$

$\Rightarrow \mathrm{AC} \times \mathrm{BO}=\mathrm{AB} \times \mathrm{BC}$

$\Rightarrow 25 r=15 \times 20$

$\Rightarrow r=\frac{15 \times 20}{25}$

$\Rightarrow r=12 \mathrm{~cm}$

Now,

Volume of the double cone so formed $=$ Volume of cone $1+$ Volume of cone 2

$=\frac{1}{3} \pi r^{2} h_{1}+\frac{1}{3} \pi r^{2} h_{2}$

$=\frac{1}{3} \pi r^{2}\left(h_{1}+h_{2}\right)$

$=\frac{1}{3} \pi r^{2} h$

$=\frac{1}{3} \times 3.14 \times 12 \times 12 \times 25$

$=3768 \mathrm{~cm}^{3}$

Also,

Surace area of the solid so formed = CAS of cone $1+$ CSA of cone 2

$=\pi r l_{1}+\pi r l_{2}$

$=\pi \mathrm{r}\left(l_{1}+l_{2}\right)$

$=\frac{22}{7} \times 12 \times(15+20)$

$=\frac{22}{7} \times 12 \times 35$

$=1320 \mathrm{~cm}^{2}$