A right circular cone is divided into three parts by trisecting its height by two planes drawn parallel to the base.

Let ABC be a right circular cone of height 3h and base radius r. This cone is cut by two planes such that AQ = QP = PO = h.

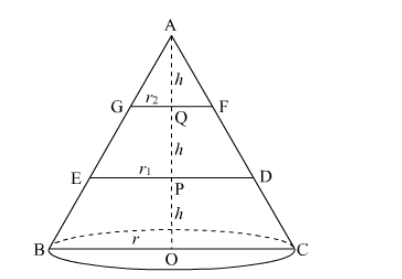
Since $\Delta \mathrm{ABO} \sim \Delta \mathrm{AEP}$ (AA Similarity)

$\therefore \frac{\mathrm{AO}}{\mathrm{AP}}=\frac{\mathrm{BO}}{\mathrm{EP}}$

$\Rightarrow \frac{3 h}{2 h}=\frac{r}{r_{1}}$

$\Rightarrow r_{1}=\frac{2 r}{3} \quad \ldots . .(1)$

Also, $\triangle \mathrm{ABO} \sim \Delta \mathrm{AGQ} \quad$ (AA Similarity)

$\therefore \frac{\mathrm{AO}}{\mathrm{AQ}}=\frac{\mathrm{BO}}{\mathrm{GQ}}$

$\Rightarrow \frac{3 h}{h}=\frac{r}{r_{2}}$

$\Rightarrow r_{2}=\frac{r}{3} \quad \ldots \ldots(2)$

Now,
Volume of cone AGF,

$V_{1}=\frac{1}{3} \pi r_{2}^{2} h$

$=\frac{1}{3} \pi\left(\frac{r}{3}\right)^{2} h \quad[$ From $(2)]$

$=\frac{1}{27} \pi r^{2} h$

Voulme of the frustum GFDE,

$V_{2}=\frac{1}{3} \pi\left(r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}\right) h$

$=\frac{1}{3} \pi\left(\frac{4 r^{2}}{9}+\frac{r^{2}}{9}+\frac{2 r^{2}}{9}\right) h \quad[$ From $(1)$ and $(2)]$

$=\frac{7}{27} \pi r^{2} h$

Voulme of the frustum EDCB,

$V_{3}=\frac{1}{3} \pi\left(r^{2}+r_{1}^{2}+r_{1} r\right) h$

$=\frac{1}{3} \pi\left(r^{2}+\frac{4 r^{2}}{9}+\frac{2 r^{2}}{3}\right) h \quad[$ From $(1)$ and $(2)]$

$=\frac{19}{27} \pi r^{2} h$

$\therefore$ Required ratio $=V_{1}: V_{2}: V_{3}=\frac{1}{27} \pi r^{2} h: \frac{7}{27} \pi r^{2} h: \frac{19}{27} \pi r^{2} h=1: 7: 19$