A rhombus whose diagonals are 4 cm and 6 cm in lengths.

Solution:

We know that, all sides of a rhombus are equal and the diagonals of a rhombus are perpendicular bisectors of one another. So, to construct a rhombus whose diagonals are 4 cm and 6 cm use the following steps.

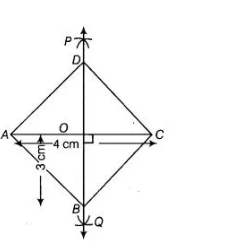
1. Draw the diagonal say AC = 4 cm
2. Taking A and C as centres and radius more than ½ AC draw arcs on both sides of the line segment AC to intersect each other.
3. Cut both arcs intersect each other at P and Q, then join PQ.
4. Let PQ intersect AC at the point O. Thus, PQ is perpendicular bisector of AC.
5. Cut off 3 cm lengths from OP and OQ, then we get points B and D.
6. Now, join AB, BC, CD, and DA .
   Thus, ABCD is the required rhombus.

Justification

Since, D and B lie on perpendicular bisector of AC.

DA = DC and BA = BC …(i)

[since, every point on perpendicular bisector of line segment is equidistant from end points

of line segment]

Now, ∠DOC = 90°

Also, OD = OB = 3 cm

Thus, AC is perpendicular bisector or BD.

CD = CB …(ii)

AB = BC =CD = DA

from Eq (i)and (ii)

ABCD is a rhombus.