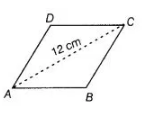
A rhombus shaped sheet with perimeter 40 cm

Let $A B C D$ be a rhombus having each side equal to $x \mathrm{~cm}$.

i.e., $\quad A B=B C=C D=D A=x \mathrm{~cm}$

Given, perimeter of a rhombus $=40$

$\therefore \quad A B+B C+C D+D A=40$

$\Rightarrow \quad x+x+x+x=40$

$\Rightarrow \quad 4 x=40$

$\Rightarrow \quad x=\frac{40}{4}$

$x=10 \mathrm{~cm}$

In $\triangle A B C$, let $a=A B=10 \mathrm{~cm}, b=B C=10 \mathrm{~cm}$

and $C=A C=12 \mathrm{~cm}$

Now, semi-perimeter of a $\triangle A B C, s=\frac{a+b+c}{2}$

$=\frac{10+10+12}{2}=\frac{32}{2}=16 \mathrm{~cm}$

$\therefore$ Area of $\triangle A B C=\sqrt{s(s-a)(s-b)(s-c)}$ [by Heron's formula]

$=\sqrt{16(16-10)(16-10)(16-12)}$

$=\sqrt{16 \times 6 \times 6 \times 4}=4 \times 6 \times 2=48 \mathrm{~cm}^{2}$

$\therefore \quad$ Area of the rhombus $=2($ Area of $\triangle A B C)=2 \times 48$

$=96 \mathrm{~cm}^{2}$

$\because$ Cost of painting of the sheet of $1 \mathrm{~cm}^{2}=₹ 5$

$\therefore$ Cost of painting of the sheet of $96 \mathrm{~cm}^{2}=96 \times 5=₹ 480$

Hence, the cost of the painting of the sheet for both sides $=2 \times 480=₹ 960$