Question:
A reservoir is in the shape of a frustum of a right circular cone. It is 8 m across at the top and 4 m across at the bottom. If it is 6 m deep, then its capacity is
(a) $176 \mathrm{~m}^{3}$
(b) $196 \mathrm{~m}^{3}$
(c) $200 \mathrm{~m}^{3}$
(d) $110 \mathrm{~m}^{3}$
Solution:
$r_{1}=\frac{8}{2}$
$=4 \mathrm{~m}$
$r_{2}=\frac{4 \mathrm{~m}}{\alpha}$
$=2 \mathrm{~m}$ and
$h=6 \mathrm{~m}$
The volume of reservoir
$=\frac{h}{3} \pi\left\{r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}\right\}$
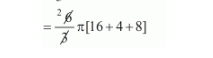
$=56 \pi$
$=56 \pi$
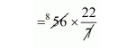
$=176 \mathrm{~m}^{2}$
The volume of reservoir = 176 m2
Hence, the correct answer is choice (a).
