A reservoir is in the shape of a frustum of a right circular cone.

Solution:

$r_{1}=\frac{8}{2}$

$=4 \mathrm{~m}$

$r_{2}=\frac{4 \mathrm{~m}}{\alpha}$

$=2 \mathrm{~m}$ and

$h=6 \mathrm{~m}$

The volume of reservoir

$=\frac{h}{3} \pi\left\{r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}\right\}$

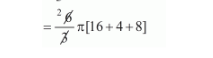
$=56 \pi$

 

$=56 \pi$

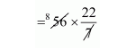
$=176 \mathrm{~m}^{2}$

The volume of reservoir = 176 m2

Hence, the correct answer is choice (a).