Question:
A ray of light coming from the point $(2,2 \sqrt{3})$ is incident at an angle $30^{\circ}$ on the line $x=1$ at the point $\mathrm{A}$. The ray gets reflected on the line $x=1$ and meets $x$-axis at the point $\mathrm{B}$. Then, the line $\mathrm{AB}$ passes through the point:
Correct Option: , 3
Solution:
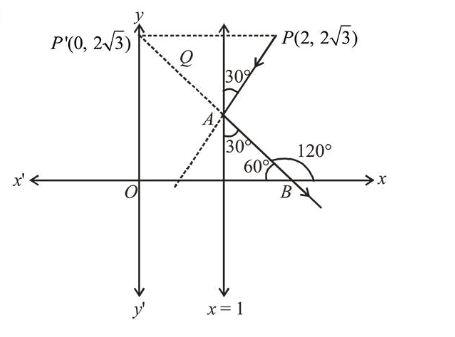
Slope of $A B=\tan 120^{\circ}=-\sqrt{3}$
$\therefore$ Equation of line $A B$ (i.e. $B P^{\prime}$ ):
$y-2 \sqrt{3}=-\sqrt{3}(x-0)$
$\Rightarrow \sqrt{3} x+y=2 \sqrt{3}$
$\therefore$ Point $(3,-\sqrt{3})$ lies on line $A B$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.