Question:
A pulse travelling on a string is represented by the function
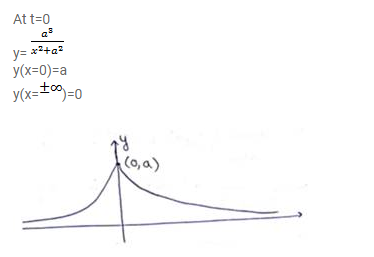
$y=\frac{a^{3}}{(x-v t)^{2}+a^{2}}$
Where $a=5 \mathrm{~mm}$ and $\mathrm{v}=20 \mathrm{~cm} / \mathrm{s}$. Sketch the shape of the string at $\mathrm{t}=0,1 \mathrm{~s}, 2 \mathrm{~s}$. Take $x=0$ in the middle of the string.
Solution: