Question:
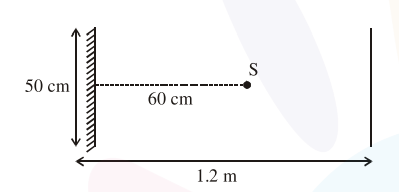
A point source of light $\mathrm{S}$, placed at a distance $60 \mathrm{~cm}$ infront of the centre of a plane mirror of width $50 \mathrm{~cm}$, hangs vertically on a wall. A man walks infront of the mirror along a line parallel to the mirror at a distance $1.2 \mathrm{~m}$ from it (see in the figure). The distance between the extreme points where he can see the image of the light source in the mirror is .......... $\mathrm{cm}$.
Solution:
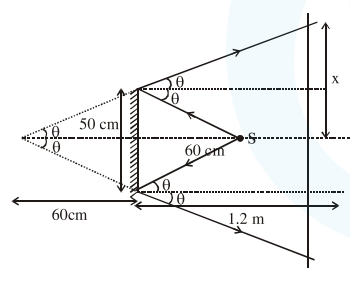
$\tan \theta=\frac{25}{60}=\frac{x}{180}$
$x=75 \mathrm{~cm}$
so distance between extreme point $=2 x=2 \times$
$75=150 \mathrm{~cm}$
