A point P is at a distance of 29 cm from the centre of a circle of radius 20 cm.

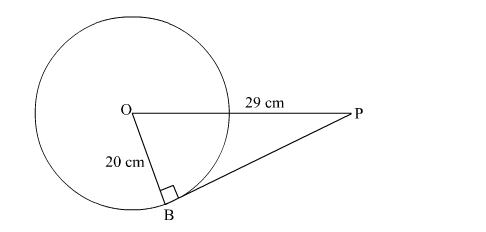
Consider the figure. 
We know that the tangent is perpendicular to the radius of a circle. 

So, $\mathrm{OPB}$ is a right angled triangle, with $\angle \mathrm{OBP}=90^{\circ}$

By using pythagoras theorem in $\triangle \mathrm{OPB}$, we get

$\Rightarrow \mathrm{OB}^{2}+\mathrm{PB}^{2}=\mathrm{OP}^{2}$

$\Rightarrow(20)^{2}+\mathrm{PB}^{2}=(29)^{2}$

$\Rightarrow 400+\mathrm{PB}^{2}=841$

$\Rightarrow \mathrm{PB}^{2}=841-400=441$

$\Rightarrow \mathrm{PB}=\sqrt{441}=21$

So, length of the tangent from point P is 21 cm.