A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see fig.).
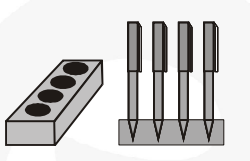
Radius of conical cavity = 0.5 cm and depth
(i.e., vertical height) = 1.4 cm
Volume of wood taken out to make one cavity
$=\frac{\mathbf{1}}{\mathbf{3}} \pi \mathbf{r}^{2} \times \mathbf{h}=\frac{\mathbf{1}}{\mathbf{3}} \times \frac{\mathbf{2 2}}{\mathbf{7}} \times(0.5)^{2} \times(1.4) \mathrm{cm}^{3}$
$=\frac{1}{3} \times \frac{22}{7} \times \frac{1}{4} \times \frac{14}{10} \mathrm{~cm}^{3}=\frac{11}{30} \mathrm{~cm}^{3}$
Volume of wood taken out to make four cavities
$=4 \times \frac{11}{30} \mathrm{~cm}^{3}=\frac{44}{30} \mathrm{~cm}^{3}$
volume of the wood in the pen stand
$=(15 \times 10 \times 3.5)-\frac{\mathbf{4 4}}{\mathbf{3 0}} \mathrm{cm}^{3}=(525-1.47) \mathrm{cm}^{3}$ (approx.) $=523.53 \mathrm{~cm}^{3}$ (approx.)
