A path of 8 m width runs around the outside of a circular park whose radius is 17 m.

(i) The radius (r) of the inner circle is 17 m.
The radius (R) of the outer circle is 25 m.          [Includes path, i.e., (17 + 8)]

Area of the path $=\pi R^{2}-\pi r^{2}$

$=\pi\left(R^{2}-r^{2}\right)$

$=\frac{22}{7}\left(25^{2}-17^{2}\right)$

$=\frac{22}{7} \times(25-17)(25+17)$

$=\frac{22}{7} \times 8 \times 42$

$=1056 \mathrm{~m}^{2}$

∴ Area of the path = 1056 m2                

(ii)

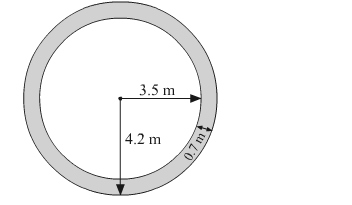
Diameter of the circular park = 7 m

$\therefore$ Radius of the circular park, $r=\frac{7}{2}=3.5 \mathrm{~m}$

Width of the path = 0.7 m
∴  Radius of the park including the path, R = 3.5 + 0.7 = 4.2 m
Area of the path

$=\pi R^{2}-\pi r^{2}$

$=\pi\left(R^{2}-r^{2}\right)$

$=\frac{22}{7}\left(4.2^{2}-3.5^{2}\right)$

$=\frac{22}{7} \times(4.2-3.5) \times(4.2+3.5)$

$=\frac{22}{7} \times 0.7 \times 7.7$

$=16.94 \mathrm{~m}^{2}$

Rate of cementing the path = Rs 110/m2      (Given)
∴ Total cost of cementing the path
= 16.94 × 110
= Rs 1863.40
Thus, the expenditure of cementing the path is Rs 1863.40.