Question:
A particle of mass $m$ moves in a circular orbit
under the central potential field, $U(\mathrm{r})=\frac{-\mathrm{C}}{\mathrm{r}}$,
where $\mathrm{C}$ is a positive constant.
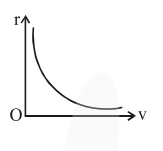
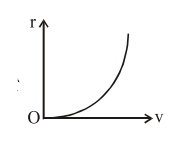
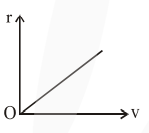
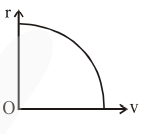
The correct radius - velocity graph of the particle's motion is :
Correct Option:
Solution:
$\mathrm{U}=-\frac{\mathrm{C}}{\mathrm{r}}$
$\mathrm{F}=-\frac{\mathrm{dU}}{\mathrm{dr}}=-\frac{\mathrm{C}}{\mathrm{r}^{2}}$
$|\mathrm{F}|=\frac{m v^{2}}{r}$
$\frac{\mathrm{C}}{\mathrm{r}^{2}}=\frac{\mathrm{mv}^{2}}{\mathrm{r}}$
$\mathrm{v}^{2} \propto \frac{1}{\mathrm{r}}$