A particle of mass $1 \mathrm{mg}$ and charge $\mathrm{q}$ is lying at the mid-point of two stationary particles kept at a distance ' $2 \mathrm{~m}$ ' when each is carrying same charge ' $q$ '. If the free charged particle is displaced from its equilibrium position through distance ' $x$ ' $(x<<1 \mathrm{~m})$. The particle executes SHM. Its angular frequency of oscillation will be __________$-\times 10^{5} \mathrm{rad} / \mathrm{s}$ if $\mathrm{q}^{2}=10 \mathrm{C}^{2}$.
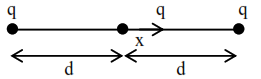
Net force on free charged particle
$\mathrm{F}=\frac{\mathrm{kq}^{2}}{(\mathrm{~d}+\mathrm{x})^{2}}-\frac{\mathrm{kq}^{2}}{(\mathrm{~d}-\mathrm{x})^{2}}$
$\mathrm{~F}=-\mathrm{kq}^{2}\left[\frac{4 \mathrm{dx}}{\left(\mathrm{d}^{2}-\mathrm{x}^{2}\right)^{2}}\right]$
$\mathrm{a}=-\frac{4 \mathrm{kq}^{2} \mathrm{~d}}{\mathrm{~m}}\left(\frac{\mathrm{x}}{\mathrm{d}^{4}}\right)$
$\mathrm{a}=-\left(\frac{4 \mathrm{kq}^{2}}{\mathrm{md}^{3}}\right) \mathrm{x}$
So, angular frequency
$\omega=\sqrt{\frac{4 \mathrm{kq}^{2}}{\mathrm{md}^{3}}}$
$\omega=\sqrt{\frac{4 \times 9 \times 10^{9} \times 10}{1 \times 10^{-6} \times 1^{3}}}$
$\omega=6 \times 10^{8} \mathrm{rad} / \mathrm{sec}$
